OCR Accuracy Metrics Without Ground Truth Data

One of the projects I pursued during my summer fellowship at the University of California San Fransisco Industry Documents Library (UCSF IDL).

Introduction

OCR Context

Optical Character Recognition, or OCR, is a heavily utilized technology with broad applications across many industries. In essence, OCR is just converting pictures of printed text or handwriting into digital text - something along the lines of a .txt file or Word document. While at face value this seems simple (probably because it’s very easy for us humans to do), in fact it is not. Think of all the situations you see text in on a daily basis - vastly different fonts, lighting conditions, rotations of the text, formats of the text, layout of the page (e.g. newspapers), and handwriting styles.

There exist a vast array of open-source and commercial OCR technologies with a wide range of capabilities. However, there exists a general dichotomy in the solutions available: highly accurate yet expensive or slow OCR vs comparatively inaccurate yet cheap or very fast OCR. Proprietary solutions such as AWS Textract fall in the expensive/slow/accurate category, while open-source solutions like Tesseract fall more in the cheap/fast/inaccurate category.

UCSF IDL Context

In the UCSF Industry Documents Library, the problem is even more complex. Text might need to be redacted, we have to deal with many file formats (e.g. pdf, tiff, Excel sheets, images, etc…), and with varying qualities of text. Some digital scans of physical documents might be very poor, grainy, have various ink stamps on them, or have any other number of issues.

Specifically relevant to the JUUL Labs and RJ Reynolds collections I focused on in my fellowship, there was a handwriting campaign that led to a huge chunk of inconsistently written and formatted letters.

The IDL has a massive database of documents to support researchers studying digital humanities around the world. In order to easily find the specific documents they are looking for, they can search the IDL website for keywords (e.g. “JUUL”, “disclosure”, or “youth”), which will go through our previously-generated OCR. This OCR was generated using older OCR technology. Much of this OCR text is fine, with most key words from the original documents being contained in the OCR text. However, some of the original OCR text is very bad and doesn’t contain key words, particularly on handwritten text. This is essential data to have, as scanned letters from a letter writing campaign compose an important portion of the dataset. If a researcher were to search for a keyword, these documents likely wouldn’t appear. It would be almost like they are invisible, inaccessible by many searches.

Modern software like Textract can get acceptable OCR for even the most illegible handwriting, but it would be unfeasibly expensive and time-consuming to re-run all documents through an algorithm like that. Most of the original OCR is fine too, so running this through Textract wouldn’t yeild as much benefit. We need some way of using the already-generated OCR, and specifically applying the more expensive algorithm in the places it is most needed, like in handwritten letters.

My Solution

In thinking about this problem, I believe that the best solution is to develop or identify a metric that can distinguish between poor quality OCR (such as that from handwriting) and acceptable OCR, perhaps with a few typos or mid-level errors (such as from scanned-in emails). This is not a trivial problem, as the poor quality OCR can have some of the trappings of reasonable English like the length of “words”, and the acceptable OCR can have some of the indicators of meaningless text (e.g. erroneous numbers, many typos, etc…).

There already exist standard metrics for testing the accuracy of OCR text such as word error rate and character error rate, but these rely on having “ground truth” text - transcriptions of the documents generated by humans that are known to be correct. We need an algorithm that can do the same, except without any ground truth data.

In this project, I identified and tested numerous algorithms on their ability to distinguish between these two types of OCR text. Many of these algorithms come from completely different areas of computer science and even mathematics, and represent many hours of research identifying and testing them. I also explore where the best of these algorithms fail, unique methods to combine them, and optimizations.

Algorithms

Autocorrect-based

The first general category of algorithms for detecting poor quality OCR was autocorrect algorithms. The main idea is to take OCR text, run it through an autocorrect algorithm, then look to see how much autocorrect changed the text. If autocorrect changed the text a whole lot, then the original text probably was of poor quality. On the other hand, if autocorrect doesn’t do much (doesn’t change many words), the text is probably high quality to begin with.

In practice, there are a few more steps. When I take in a file with OCR text, I first split it into lines. Then, I apply a normalizer algorithm (whisper’s EnglishTextNormalizer). This reduces text to lower case and performs other normalization steps to make the autocorrect effects more consistent. Many files contain numerous empty lines, and some autocorrect algorithms also do not work on them. So to mitigate this, I map ever totally empty line to an arbitrary string that never appears in text and will not be changed by autocorrect (in my case I used “1111111111111111”). Thus, new lines will always equal new lines in the normalized and the normalized + autocorrected text, without causing errors if the autocorrect algorithm doesn’t accept empty new lines.

Then the process diverges. These normalized lines are saved, and another version is fed through the autocorrect algorithm. Finally, I compare each normalized line to its corresponding normalized + autocorrected version using a word error rate (WER) algorithm (I use jiwer.wer) and place the WER for each line in a new array. WER measures the proportion of words containing errors to the total numer of words. A high WER means the text is low quality, and a low WER means the text is high quality. I then average the WERs and return this value as the final error for this file and this particular autocorrect algorithm.

In this category, I tested two Python libraries: autocorrect and jamspell.

Autocorrect Library

Autocorrect is (https://github.com/filyp/autocorrect), a multilingual spelling corrector based on the older autocorrect library and Peter Norvig’s spelling corrector (https://norvig.com/spell-correct.html). This algorithm uses the Levenshtein distance (also called the edit distance), which calculates the number of edits it takes to change one word to another word, to determine the word from a corpus closest to misspelled words, and correcting the misspelled word to that word. When a misspelled word could potentially be converted to multiple known words with the same edit distance, it chooses the most common target word in the corpus.

The library autocorrect also has a few other features which I tested. It has a fast mode, that only detects single typos (e.g. edit distance of 1), and also an OCR-specific mode that only uses edits based on replacements, as these are particularly common for OCR text (e.g. amount is OCR-ed as omount). I tested every combination of these features (standard autocorrect, OCR-mode, fast mode, and OCR + fast mode)

These could be helpful, as speed is of the essence for our project. We want our algorithm to save time and money, and as such it has to be able to process thousands of documents very quickly. Anything that reduces computation time a tiny bit will correspond to a huge improvement when run on thousands of documents.

Jamspell Library

Jamspell (https://github.com/bakwc/JamSpell) is another autocorrection library focusing on accuracy, speed, and cross-platform availability. It is a more modern and advanced library, utilizing an N-gram markov model to context-specific achieve accuracy, and implements a number of optimizations (such as a Bloom filter) over its predecessor SymSpell. I expected this algorithm to perform better than the more basic autocorrect library.

Gibberish Detectors

The second major category of algorithms I used was gibberish detectors. Gibberish can actually be a significant problem for those who host and manage websites and web services, as malicious users can automatically submit random queries to occupy the server and slow down other users. In some cases, each user query costs the website a tiny amount of money, and random queries could become extremely expensive. In a similar scenario, malicious users of forum websites like Reddit could automatically submit many junk posts.

Thus, numerous tools have already been developed to quickly detect gibberish text quickly and very efficiently, as a computationally expensive gibberish detector could impose more strain on servers than a junk query.

For these, I tested three tools: gibberish-detector, autonlp_gibberish_detector, nostril, and random_string_detector. For each, I run the algorithm through a similar process as described above, where I split the text into lines, pass each line to the gibberish detector, and average the scores into a final gibberish score. For detectors that return one True/False value, I return the proportion of gibberish lines. While this is not a perfect way of generating metrics, it is more than sufficient and is very efficient.

Gibberish-Detector

Gibberish-Detector (https://github.com/amitness/Gibberish-Detector) is a Python program forked from rrenaud’s algorithm of the same name (https://github.com/rrenaud/Gibberish-Detector), modified to support Python 3 and using a 3-character markov chain model instead of rrenaud’s 2-character model (Random-String-Detector also uses a 2-gram model. This model returns a True/False value.

Markov models are the precursors to modern neural networks, in this scenario they work by training on a corpus of correct English text (such as Wikipedia), and record how often each sequence of n characters (n = 3 in the case of amitness’ Gibberish-Detector). Then, when the model sees new text, it calculates the probability of seeing each sequence of n characters in the text and multiplies them all together. If this probability per character is below a cutoff value (which can be optimized, as I will discuss later), then the text is marked as gibberish. A lot probability per character score would align with strange text that was not commonly seen in the original corpus of example text.

As an implementation note, Gibberish-Detector is not a Python library or module, and is two Python programs and a compressed file of frequencies. This made it slightly harder to run from Google Colab. To make this easier I downloaded the relevant files into my Google Drive which I then connected to Colab, to allow for file persistence. Then, I imported the Python file’s methods from inside my main Google Colab notebook.

Autonlp-Gibberish-Detector

Autonlp-Gibberish-Detector (https://huggingface.co/madhurjindal/autonlp-Gibberish-Detector-492513457) uses a neural classifier model to identify text as either gibberish or reasonable English. Like the Markov models some of the previously described algorithms use, neural networks have to be trained on a corpus. In classifiers like Autonlp-Gibberish-Detector, the corpus must be labeled, meaning that the corpus consists of some gibberish text that we know is gibberish text, and some text that is known to be correct. During training the classifier makes an educated guess as to which category text in the corpus belongs to, and then we correct it’s guess and modify the model to be more likely to generate the correct answer next time.

Neural models like Autonlp-Gibberish-Detector return a confidence score as to whether the text is gibberish or not, and I use the average of this score directly.

Nostril

Nostril (https://github.com/casics/nostril), or the Nonsense String Evaluator, is a Python module that provides a convenient function that returns a True/False value as to whether the the input text (a short string) is gibberish text or not. This model was actually specifically trained on source code to identify meaningful identifiers like variable and function names, but it actually works quite well on standard English text.

Nostril works by using heuristics to detect simple True/False cases, and an TF-IDF scoring system based on 4-grams for more complex cases, described in the paper “Nostril: A nonsense string evaluator written in Python” (https://joss.theoj.org/papers/10.21105/joss.00596). This is similar to the Markov models described above, but with an added caveat that TD-IDF adjusts the frequency lists based on both the frequency of n-grams within one document, but also across all documents in the training set.

In the implementation of this algorithm, I came across the problem that Nostril will refuse to evaluate very short strings (less than 6 characters). This is a problem for lines that contain fewer than 6 characters, as Nostril will throw an error. To account for this, I simply caught any errors that Nostril produced and marked that line as nonsense. While again this is a very rudimentary metric, it is quick and leads to quite good results.

Random-string-detector

This is a Python library that uses a 2-gram (bigram) model, like Gibberish-Detector but with less context information. I expected that this library would perform worse than Gibberish-Detector as it used a 2-gram model compared to a 3-gram model, but that it might also be faster. This library returns a True/False value.

Mathematical

This general category encompasses mathematical methods for detecting gibberish text. Here I analyzed two metrics: the index of coincidence and the character entropy. These methods are generally quick, and I wanted to test their accuracy compared to the specifically designed gibberish detection algorithms.

Index of Coincidence

The index of coincidence (IC) is a metric originally from cryptography to detect correct decryption of ciphertext. The IC of a string is also not affected by substitution ciphers (where each unique character of plaintext is mapped to unique ciphertext character).

It measures the probability of pulling two random characters from a text and getting the same one. The probability of pulling the first letter is n / L, where n is the count of how many times the target character appears in our text, and L is the total number of characters in the text. The probability of pulling the second letter is (n-1) / (L-1), as by pulling the first letter out, we have reduced both the number of our target characters, and the total number of characters in the text. To calculate the IC of a specific character, we multiply these two values together ((n/L) * ((n-1)/(L-1)). To calculate the IC of a whole text, we calculate the average IC of all characters contained in the text.

The idea of the IC is that for random or gibberish text, each character is about evenly distributed as as such the IC for that text will be close to 1. For text in English or any other language, characters are not evenly distributed so the IC will be somewhat greater than 1, somewhere around 1.7. Notably, my algorithm normalizes text to be lowercase and counts all characters present in the text except spaces and new lines (even numbers, punctuation, and symbols). This differs a bit from its original usage where ciphertext and plaintext would usually only contain letters. As such the IC values for my text can sometimes be over 2, but gibberish text still has an IC value of about 1.

This is a relatively simple algorithm to implement with a dictionary in Python, which is an efficient data structure that allows this algorithm to run very quickly.

Character Entropy

Character entropy as I am using the term here refers to the entropy of the distribution of characters in a document. I am using Shannon’s definition of entropy of the distribution of a quantity (such as the frequency of letters) to be the average of (-1 * p * log(p)), where f is the proportion of text taken up by each character. A low entropy means the text is very predictable, while a high entropy means the text is difficult to predict.

I’ve seen this metric used in an attempt to determine whether or not the Voynich Manuscript represents meaningful language or is a hoax (apparently the language has a significantly lower character entropy than languages we know to be real).

As a note, in my implementation of this, I do not count spaces.

LLM-based

The final general category I investigated (though not extensively) was LLM-based gibberish identification. LLMs, at a high level, work by predicting a probability distribution for the next token (part of a word) based on previous tokens. LLMs like ChatGPT take your prompt and continuously select the next token according to this probability distribution.

I take advantage of this for identifying nonsense text by tokenizing (splitting the text into tokens) each line and measuring the perplexity of GPT-2 on that line (any language model would do, but I wanted something relatively lightweight). Perplexity is e to the power of the loss per token of input text of the model. Loss is how “incorrect” or how “surprised” the model is by the next token. I averaged the perplexity of each line of the file. High perplexity means the text is very “confusing” - that it doesn’t look like anything it has seen before - that it is gibberish.

In the implementation of this algorithm, I initially got exemplary results: extremely quick and very accurate. This made me a bit suspicious as LLMs are generally somewhat slow, plus I was running GPT-2 on Google Colab without huge computational resources so it would likely be even slower. Upon investigation, I realized that I had been passing in the file name instead of the file text to GPT-2. Somehow, the file name is highly correlated with whether the document is good OCR or bad OCR.

After fixing this error, the perplexity-based metric was extremely slow and gave frequent errors. LLMs have maximum context sizes - the maximum number of tokens they can process in one run - and I was exceeding it for some longer lines. This gave frequent errors that I caught and recorded. The metric was the slowest by far (taking over 4 hours to run on 160 documents) and it wasn’t even very accurate. As a result of this poor initial performance, extreme length of tests which limited me from running other code on Google Colab, and the outstanding performance of other metrics, I decided not to pursue LLM-based metrics any further.

Experimental Method

Testing metrics

Each of the algorithms above generated a somewhat continuous metric. The ones that inherently returned True/False were modified as described above to produce a proportion of gibberish between 0 and 1. Some algorithms similarly generated scores between 0 and 1, while others generated numbers that were smaller or larger.

The data I had available were the JUUL hot 60 documents (mostly PDFs of emails, word documents, Excel sheets, and other things that have accurate OCR), and the RJ Reynolds 100 handwritten documents, which mostly contained handwritten letters which have very poor OCR transcriptions. Every document has an OCR file associated with it, run previously with older technology.

I took advantage of this pre-labeled data by assuming that the JUUL documents were good OCR, and the RJR documents were bad OCR. This is not strictly true, but it is a fair approximation based on the data we already have.

For each metric, I ran every bad OCR file and every good OCR file through it, and recorded this result in dictionaries based on whether the origin file (the key is the name of the file, the value is the metric score). Errors in processing (such as GPT-2 running out of tokens) were recorded as value = -1. Then, I normalized those scores to be between 0 and 1 by dividing each score by the maximum score I calculated for that metric. It is possible that running this algorithm on future text would generate scores greater than 1, but this doesn’t affect anything due to the cutoffs which I will describe shortly. Errors were converted to either 0 or 1, and for every metric I tested which value was better for errors.

Now, for every metric I have two dictionaries: one containing the scores when ran on the bad OCR documents, and one when run on the good OCR documents. I could compare the average metric scores between the two categories, but this isn’t actually very useful in the real world. We really want a decision function that when a metric is passed as input, it outputs True if the text is good OCR, and False if the text is bad OCR. This function and its optimization is described below. For now, I will assume that we have such a function.

Then, I iterate through every file in the dictionary and run this decision function on the metric score. I then take the proportion of files that it correctly sorts and return this as the final accuracy of that metric.

Decision functions

The individual metrics generate one-dimensional outputs (just one number between 0 and 1). Thus, the best decision function will be a hard cutoff. Any value below the cutoff will be labeled good OCR, and any value above the cutoff will be labeled bad OCR. Whether good OCR is above or below the cutoff is actually arbitrary and will not affect the final accuracy of the metric, but it will invert whether high scores = good OCR or high scores = bad OCR.

OK so now we know the general format of the decision function: a hard cutoff. But how can we optimize this cutoff? One solution is to iterate through every possible cutoff between 0 and 1, and test how many the model got correct. However, this would require testing an infinite number of points (infeasible). Another idea would be to test cutoffs all spaced 0.001 (or any other arbitrarily small number) apart. Yet again, this would be inefficient and slow. The solution I employed is to test every value each metric generated as a potential cutoff point. This would still generate the optimal cutoff for our specific dataset, but the best cutoff might be slightly different in the real world.

This cutoff point could then be tweaked up or down manually to select for more false positives or false negatives, depending on the needs of the user.

Testing Environment

All tests were run on the free tier of Google Colab. This did pose occasional problems for the slower metrics, as Colab will automatically disconnect you after a certain period of inactivity (even while code is running). However, this was relatively minor. I was on a Python 3 CPU runtime with 12.7 GB of RAM and 107.7 GB of disk space. It’s likely that these computation times could be sped up by multithreading, but I did not experiment with this.

Results

Some decision functions generate higher scores for good OCR documents, while others generate higher scores for bad OCR documents. For example, my GPT-2 based metric would score the worst possible OCR text as a 1 and the most perfect OCR as a 0, while Nostril would score perfect OCR as a 1 and absolutely horrible OCR as a 0. I have separated the two below. If a number is in the “Accuracy, printed < handwritten” column, then the metric is higher for handwritten (poor quality) text, whereas if it is in the “Accuracy, printed > handwriting” column, then the metric is greater for printed (good quality) text.

The time in seconds taken for each algorithm to run through the 160 documents, the average time in seconds to run on one document, and the time in days to run through about 19.971 million documents is shown to the far right of the table. The time taken to run through about 20 million documents was included, as this is the total number of documents in the UCSF IDL (it may have changed by the time you are reading this, so I would recommend checking https://www.industrydocuments.ucsf.edu/about/overview/).

	0 or 1 better for errors	Accuracy, printed < handwriting	Accuracy, printed > handwriting	time (sec) for 160 docs	time (sec) per doc	days / 19,971,203
Autocorrect-based
Autocorrect	1	0.79375		3586.791576	22.41744735	5181.752219
Autocorrect (ocr)	1	0.73125		1030.272014	6.439200085	1488.409399
Autocorrect (fast)	1	0.7125		168.904669	1.055654182	244.0125458
Autocorrect (ocr fast)	1	0.775		156.159615	0.975997594	225.6000703
Jamspell	1	0.875		317.2893317	1.983058323	458.3803279
Gibberish Detection
Gibberish-Detector	1	0.89375		5.288775206	0.03305484504	7.640567365
Autonlp Gibberish Detector	0		0.84375	7745.523014	48.40951883	11189.77231
Nostril	1	0.975		8.434419632	0.0527151227	12.18500482
Random-String-Detector	1	0.85625		3.110783577	0.01944239736	4.494074819
Mathematical
Character Entropy	0		0.79375	2.986999273	0.01866874546	4.315246589
Index of Coincedence	1	0.88125		3.169683456	0.0198105216	4.57916607
LLM-based
GPT-2	0		0.8466666667	14659.70946	91.62318412	21178.53252

Conclusion & Discussion

Overall, the most accurate metric was Nostril by far, achieving an accuracy of 97.5%. This means that out of the 160 documents, it only for 4 incorrect. Other metrics such as Jamspell, index of coincidence, and Gibberish-Detector also did well, with accuracies significantly over 80%. Nostril was reasonably fast and very accurate, but the index of coincidence struck a very good balance between speed and accuracy. It is extremely important to note that this doesn’t exactly mean that we can distinguish between handwriting and printed text 97.5% of the time, only that we can distinguish between these two collections with 97.5% accuracy, which may or may not translate to larger or different samples. For example, we compared mostly printed text to pue handwriting, and this sort of pure handwriting is a small percentage of the overall data. Many documents are some mix of handwriting and printed text, and we would likely detect these as “good OCR”. In fact though, the handwritten information may be the most useful part of the document, such as in printed forms where all the interesting information is handwritten in. While lowering the cutoff may be able to detect some of these documents, future investigations on mixed handwriting & printed documents are necessary to confirm. The results of one such investigation are described below.

It is interesting to observe that 1 is a better value for errors when printed < handwriting, while 0 is better for errors when the opposite is true. This makes intuitive sense, as an error likely indicates poor quality text, and 1 represents the worst possible quality text when the metric is higher for handwritten (poor quality) text compared to printed (high quality) text.

Evaluation on Randomly selected IDL Data

To test the generalizability of these metrics, I ran 3 promising metrics on a randomly selected set of about 30,000 documents from the Industry Documents Library I scraped from the public library. The reason I didn’t run any more due to time constraints. I wanted to see how well these metrics would be able to distinguish between high and low-quality OCR. However, there aren’t labeled datasets like there were for the JUUL data. So, in order to evaluate these metrics, we can look at the distribution of scores. If a metric were very good at separating high and low-quality OCR, we would hope to see a bimodal distribution, making separating the two sets easy. Additionally, we’d like a metric that can generate a number as often as possible, and not fail often. Thus, I also include the percent of the time the accuracy generated a value.

Looking at the graphs below, it is clear that Nostril has the most bimodal distribution. The metric score is on the x-axis, and the count of how many documents fell into that bucket is on the y-axis. This is even further evidence that this is the most robust and balanced metric.

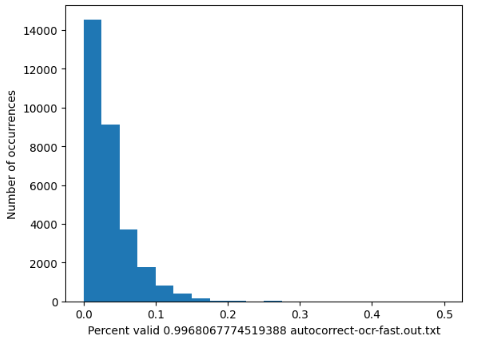
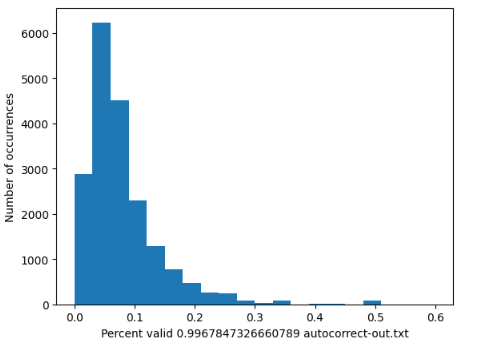
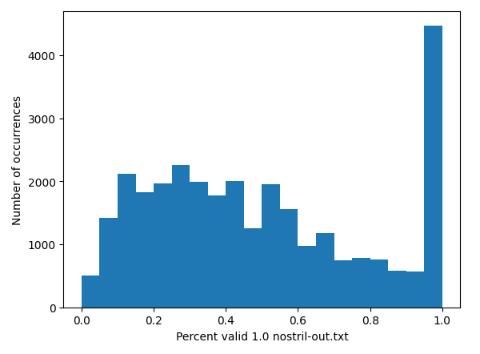
Category Comparison and the Time/Accuracy Trade-off

Some categories performed remarkably better than others. Autocorrect-based algorithms were the worst of the categories, often failing to reach 80% accuracy. I believe this is because these algorithms essentially “gave up” correcting extremely bad OCR, which is what most of the RJR handwritten documents are. The autocorrect can’t correct single letters or totally meaningless symbols, so oftentimes the autocorrect algorithms didn’t change much of the bad OCR text. These algorithms were also extremely slow, and the more accurate algorithm Jamspell was slower then the second and third best performers in this category.

Gibberish detection algorithms performed the best, with the two best performers being in this category. These algorithms were much faster than the autocorrect-based metrics, but within this category we yet again see a tradeoff between time taken and accuracy. While Nostril was the most accurate algorithm, it was not the quickest in the category (this title goes to Random-String-Detector, which was almost 3 times quicker than Nostril).

The mathematical category performed surprisingly well, better than the autocorrect-based algorithms but marginally worse than the gibberish detection algorithms. The third best algorithm (index of coincedence) is in this category. What they lose in accuracy, they make up for in speed. These algorithms take only one pass through the text to count the occurrences each character, then perform one calculation per character.

The LLM category performed acceptably well, but took an extremely long time, eliminating this group as a candidate for large-scale gibberish detection.

While there is no one best algorithm for every use case, it is my opinion that the index of coincidence is the best compromise between speed and accuracy, especially when applied to large datasets. For smaller datasets, one could afford to spend a bit more time running the more accurate Nostril algorithm.

Error Analysis

Keep in mind that these algorithms have not been optimized any further for speed. Multi-threading would likely speed up all of these algorithms.

I am primarily going to investigate the errors that Nostril, random-string-detector, and the index of coincidence make. I have listed each document that each of these algorithms get wrong according to my cutoff decision function, as well as some commentary. For the documents with no listed commentary, I don’t have a theory as to why that document was marked incorrect. For the documents where the score was very close to the cutoff, I have also marked this.

As shown below, the two other most promising algorithms get many of the same documents as Nostril incorrect, although their errors don’t necessarily overlap with each other as much. One of the four documents that Nostril got “incorrect” was arguably a mistake in the dataset, as it mostly contains printed text. Additionally, some of the incorrectly labeled files are Excel files, hinting at a deeper error with how the original OCR algorithm handled these files.

It is interesting to note that these algorithms are getting the scan of an email or two incorrect. these scans seem generally clean, and this is worth some further investigation.

Nostril

Printed documents Nostril incorrectly identifies as bad OCR mjxw0291 - This is a Excel file (not a PDF or other easily OCR-able format) sgxd0283 - I think this is happening because there are a lot of lines with only email addresses, strange numbers, and names. There is also a bit of clutter Handwritten documents Nostril incorrectly identifies as good OCR lghl0187 fqdx0231 - This is a printed PDF (incorrectly labeled as handwritten)

Random-String-Detector

Printed documents random-string-detector incorrectly identifies as bad OCR

mjxw0291 - Excel file (same one Nostril gets wrong)

stcx0287 - close to cutoff - clutter and images

ffdh0295 - close to cutoff - charts and a very bad scan

sgxd0283 - The same Nostril is getting wrong

rtmy0286 - close to cutoff - chart

kxmw0301 - not a very good scan

qtyw0301 - extremely close to cutoff

nlmw0301 - many images

mhmj0300

Handwritten documents random-string-detector incorrectly identifies as good OCR

ptfj0224

psdx0231

jtbj0224 - extremely close to cutoff - mix of printed & handwritten

mhjm0221

hglb0233 - extremely close to cutoff

kgwm0187 - extremely close to cutoff

ysdl0187 - mix of printed / handwritten

lghl0187 - The same one Nostril is getting wrong

zfxl0187 - close to cutoff - somewhat neat handwritten numbers

fqdx0231 - This is a pdf, the same one Nostril is getting wrong

frcp0189 - extremely close to cutoff - mix of handwriting and printed

xqyh0233 - mix of handwritten and printed

fyvp0189 - mix of handwritten and printed

gjwm0187

Index of Coincidence

Printed documents the Index of Coincidence algorithm incorrectly identifies as bad OCR

mjxw0291 - Close to cutoff, Excel file (same as Nostril)

sgxd0283 - Close to cutoff, same one Nostril gets wrong

plxd0283 - Close to cutoff, small text

gzcg0299 - Close to cutoff, a lot of images and diagrams

yqwp0298 - Close to cutoff, images

rpkg0299 - Close to cutoff, excel file

qrdg0299 - Close to cutoff, images and diagrams

Printed documents Index of Coincidence algorithmincorrectly identifies as bad OCR

mjpl0226 - Close to cutoff, relatively neat handwriting

tjpl0226

yjpl0226 - Mix of handwriting and printed text

ksyf0019 - Neat handwriting

ptfj0224

skmh0225

mhjm0221

llbj0224

xxhl0187

gqmb0233

fqdx0231 - Close to cutoff, same as Nostril gets wrong

pgwl0187 - Neat handwriting

Ensemble Method - Multiple Metrics

One potential idea is to create a combination of metrics that could potentially score higher than any one metric. We could run multiple metrics on a text, and take a weighted average over these scores.

This would only be beneficial if the documents that our best metric identifies incorrectly are documents that other metrics identify correctly. However, in analyzing the incorrect results of Nostril, Random-String-Detector, and other top performers, the documents that Nostril were identifying incorrectly were also identified incorrectly by the other algorithms.

Another limitation is in the total time required to run these metrics. Our goal is to save time and money, and running 10 computationally expensive metrics wouldn’t do either of those things. The final blow to combinations of metrics is done when considering the potential benefit: 2.5%. The absolute worst an optimized weighted combination of metrics could do is 97.5% correct, and the absolute best it could do is 100% correct. Keep in mind that 2 of the 4 documents that contribute to that remaining 2.5% were actually correctly categorized when we looked back at them.

So at best, it’s possible we might be able to improve our performance by 2.5% maybe, at the cost of spending 2 times as much computational time. I actually tested this with 2 metric combinations, and I could not generate an increase in accuracy at all.

Reflection

This project, while it seems simple at first, actually took quite a long time. Researching and identifying vastly algorithms from many different areas of CS and math was challenging, leading me down many rabbit holes. Another challenge was getting everything working. I unfortunately could not include one or two algorithms, as I could not get them running in Google Colab. Many of my initial hypotheses and ideas (e.g. using autocorrect algorithms) were ultimately not correct. There were also barriers around downloading and accessing documents programmatically, which inadvertently resulted in the discovery of a minor bug.

I would also like to test these methods on documents that contain mixed handwriting and printed text, as these are the majority of documents with handwriting in the UCSF IDL database.

I think this project was valuable, as it taught me a lot about the research process, utilizing Google Colab, and about designing and executing independent projects generally. Being almost completely independent, I was able to decide the point to stop investigating. Actually similar to the cutoff function I used, I needed some way of determining at what point my current research was “good enough”. If I didn’t have a cutoff, a project like this could go on for weeks, with only marginal improvements being made. I quite enjoyed the freedom, and I’m proud of the work I did.